Black Holes are a Thousand Times Weirder than You Think

In the depths of space, there are objects that undermine everything we feel we know about space and time. These objects are black holes.

A realistic depiction of what a black hole would look like up close, using the universe simulator Space Engine.

A black hole forms when an amount of matter is squeezed smaller than its Schwarzschild radius, the size at which its gravity is so strong that nothing, including light, can escape. When this happens, an event horizon forms at the S-radius, and the matter inside collapses to form a singularity. We’ll get a feel for what these mean as this post goes on.

The incredible amount an object must be compressed to form a black hole is staggering. In order to turn the sun into a black hole, we would have to crush it down to 6 kilometers across. That’s the total distance I walked every day to and from my university when I was in graduate school. If you were to compress the Earth into a black hole, it would be the size of a marble. If you didn’t have to worry about it tearing you apart, you could hold it in the palm of your hand.

Why do black holes look the way they do? Let’s start with a lone black hole in the cold depths of space. Since light can’t escape, it looks like a circle of blackness, and because the strength of their gravity is so great that they bend light around them, they distort the stars behind them like a lens.

From the YouTube video, “Colonizing Black Holes,” by Isaac Arthur

When a black hole is feeding on material around it, perhaps from a companion star or an object that came too close to it and was torn apart, it gets an accretion disk. Why does a disk form, rather than all the matter just falling in? There are two reasons working together. First, we have angular momentum. The matter isn’t falling straight into the black hole, but orbiting around it at insanely high speeds. Because of this, any stray matter that collides with the disk becomes part of the disk. Secondly, as the matter gets closer to the black hole, it crams together and can only go in so much at a time, like sand trickling through an hourglass.

An artist's impression of an accreting black hole. From Wikipedia

We can see an example of angular momentum creating a disk in the above artist’s rendition of a black hole accreting matter from a companion star. The star and black hole are revolving around each other, so the stream going from the star to the accretion disk curves in the forward direction, partially because of the star’s inertia, and partially because the black hole moves out of the way and the stream has to catch up.

With all that matter spiraling inward, feeding black holes build up quite the magnetic field. This magnetic field points outward from the poles, so instead of falling into the event horizon, some of the matter gets shot away at extreme speeds by these magnetic fields in two jets, as can be seen in the above picture.

As the matter in the disk crams together, it heats up due to friction, which causes the accretion disk to glow. The closer to the center, the hotter it gets, making it go from red on the outside to white on the inside. Because of how fast it is revolving, the light gets Doppler shifted, brighter and whiter on the side moving toward us, and dimmer and redder on the side moving away from us. This is heightened by the fact that the disk is spinning close to the speed of light.

A realistic depiction of a black hole up close, from the movie, Interstellar

You might notice that there is a halo around the event horizon. That’s an illusion, an image of the accretion disk on the back side of the black hole, which we can see both above and below it because of the light bending around the event horizon.

Up until 2015, we didn’t have direct observations of black holes. Now we do, first by gravitational waves with LIGO, and then a few years later by the Event Horizon Telescope, a composite telescope that uses advanced techniques to put together data from observatories all over the world, giving us an effective dish size as big as the entire Earth. Here is what that image, given artificial color, looks like.

The supermassive black hole at the center of galaxy M87.

The black circle in the center is the shadow, a blown-up view of the entire event horizon, front and back, because of the way light bends around it. If you could see it without any lensing effects, the event horizon would be a fraction of its size. There is a great YouTube video by Veritasium explaining this in more detail.

Black holes look cool, and a lot of interesting science goes into why the look like they do. But there’s more, oh so much more. So now it’s time to get to the good stuff: what black holes do to space and time. In order to discuss this, we have to be comfortable with space-time relativity, the principle that space and time are parts of the same thing, and this space-time can be curved and stretched. We talked about this in our discussion of faster-than-light travel and time travel, but here’s a little refresher.

When drawing space-time diagrams, we draw one dimension of space on the horizontal axis, and time on the vertical axis. An object sitting still will move straight up on the diagram, parallel to the time axis. An object moving will travel at a diagonal angle. We scale the plot so that light beams travel at 45-degree angles.

We choose a point to be the origin of the plot, which we call “here and now.” This could be you, it could be a space ship, a rock, or just a random point in space-time. From this point, we draw the light beams that go out into the future and come in from the past. If you imagine a third axis pointing out of the screen, these light beams circle around the time axis, making cones, which we call the past and future light cones. In reality, there is also a third dimension of space, making it a hypercone, but it is very hard to visualize four dimensions, so we talk about light cones.

From Wikipedia

No matter where you are or what the space-time curvature around you looks like, your light cone looks like this diagram. But someone else’s light cone at a different point in space could be distorted compared to your coordinate system. For instance, if we are in normal space far away from a black hole, then the light cone of something falling into a black hole curves to point toward the event horizon. And after an object has passed the event horizon, its entire light cone points toward the singularity. There is no direction it could go that would not end up at the singularity.

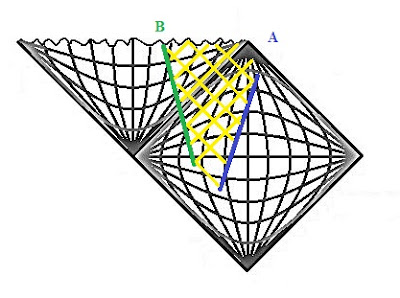
This is confusing, and not good for calculating. A much better and more intuitive way to understand black holes is with a Penrose diagram. To make a Penrose diagram, we use a math trick to change our coordinates so that we compress all of space-time into a diamond. The two bottom edges of the diamond are infinitely far back in time, and the top right is where time reaches future infinity. The top left is the event horizon of the black hole. On the other side of the event horizon, we join another half-diamond, representing the inside of the black hole.

In this diagram, lines of constant position and constant time are curved. Yet light always moves at 45-degree angles, making it easy to tell what observers in each region would see. Imagine two people, person A staying outside, person B falling in, sending signals to each other. To A outside, it would take an infinite amount of time for B to reach the event horizon, and A could keep receiving signals from B forever. However, in B’s reference frame, B passes the event horizon in a finite amount of time no problem. Then, a short time later, B reaches the singularity. Contrary to popular myth, B does not see the entire future of the universe, as we can see from the following diagram.

The paths of A and B exchanging light beams as they go. Everything moves upward, because that is the direction of time. As we can see, once B passes the event horizon, their light beams end at the singularity. B can receive signals from A, but there comes a point when A’s signals reach the singularity without reaching B first.

With a Penrose diagram, we can see a startling conclusion: inside the black hole, space and time have switched places! The singularity is no longer a point in space, but a moment in time, which all things inside the event horizon move inexorably toward. In addition, according to an observer outside the event horizon, everything that happens inside takes place after an infinite amount of time has passed!

Have a moment’s rest before we continue on. What, did you think that was as crazy as it gets? We haven’t even gotten to wormholes yet.

To get there, we first have to talk about spin. Everything floating in free space has a little bit of angular momentum, its outer parts rotating around its center of mass. Black holes are no different; the matter that forms and feeds them spirals in, contributing to their angular momentum. As a result, black holes have a property called spin. This spin prevents the matter from falling all the way to a single point, as the closer it gets the more centrifugal inertia it has to counteract the gravity. What this means is that the singularity is not a point, but a ring of zero thickness. If the spin is so high that the radius of the ring is larger than its Schwarzschild radius, then there is no event horizon, and it is called a naked singularity. Currently, no naked singularities are known to exist.

A simulation of what a naked singularity would look like from above.

If mass distorts space-time, do black holes pull space around them as they spin? Yes, they do. It’s called “frame dragging,” a name as cool as the phenomenon it describes. If we were to drop something directly toward a black hole near its plane of rotation, it would spiral around the black hole as it fell, due to the motion of space itself. There is a region near the event horizon called the ergosphere, where space is pulled so fast that an object has to travel faster than light in the opposite direction just to stay in the same place. The ergosphere is outside the event horizon, so in principle it is possible to send a ship or a probe into it and back out again. Now that would be a trip!

From Wikipedia

All right, now we’re ready to get to wormholes. Since black hole singularities are rings, it stands to reason that it’s possible to go through it. What happens? Well, you might think you just end up on the other side of the ring. After all, that’s what happens when you pass through any other kind of ring. But something weird happens. When you were a child, did you ever imagine you could go around a lamp post or a tree and find yourself somewhere else? That’s what happens when you pass through a ring singularity. Let’s look at the Penrose diagram:

With a path through the singularity, we can see that there is another side. When we get there, instead of the other side of the black hole, we find something called a white hole, an object with repulsive gravity and an event horizon nothing can get into. No one knows if white holes exist, and we don’t know of anything that has repulsive gravity. Thus, we have a one-way wormhole, with a black hole on one side nothing can get out of, and a white hole on the other side nothing can get into. What is on the other side? It could be a different place in the universe, maybe at a different time. Or, it could be another universe altogether, a space-time continuum completely separate from ours except for this one bridge.

We have never seen a white hole. This does not bode well for the possibility of their existence, since they would probably be extremely bright, launching out everything that fell into their black hole partner at relativistic speeds. Except, well, maybe we have. There is one thing that had a singularity and looks kind of what we’d expect a white hole to look like: the big bang. It’s common to think of the big bang as the beginning of everything, including time, but it might not be. Maybe it was the result of a black hole in another universe. This may seem like nothing more than sci-fi fancy, but there are a few high-profile physicists who take the possibility seriously.

So there we go, a glimpse into the depths of the weirdness of black holes. There is one more thing I’d like to say: we don’t actually know much about singularities. When we try to apply our best theories to them, General Relativity and Quantum Field Theory, we get unsolvable problems. In order to be able to model singularities, we need a theory of quantum gravity. Our two major contenders, String Theory and Quantum Loop Gravity, have both made predictions that turned out to be false. So the final tidbit of black hole weirdness I’ll leave you with is that there is still a feature about them, the singularity, that we know basically nothing about. I hope you sleep well tonight. See you next time.

The Is-Ought Gap

Some time ago, I wrote a series on morality. My approach was to go through a bunch of different views people have on morality, and give my opinions on each one, pointing out contradictions where I saw them, and picking out my favorites. Now, we’ll revisit the topic from a perspective outside the narratives, which in philosophical terms is called meta-ethics. We’ll be less concerned with which ideas are better than which, and focus on descriptions of moral behavior and ideas, and objective frameworks from which to think about it. To kick things off, we’ll talk about the is-ought gap.

The is-ought gap came from an observation by the philosopher David Hume, who noticed that every time a moral philosopher tried argue for a moral system, they would make a bunch of is-statements about the world, and somewhere along the line take a magical leap to ought-statements. For instance, “The result of evolution by natural selection is to pass on genetic information to the next generation. Therefore, we ought to live in the way that maximizes the chance of our genetic information surviving into the future.” Most of us are not satisfied with this conclusion. What about being kind to strangers? What about lifting people on the other side of the world out of poverty? That’s not the point, though. The problem is that the argument sets up an is-statement, which seems to be leading somewhere, but then jumps to an ought-statement, which does not automatically follow from it.

Another example is the nature of conscious experience. “It is the case that we all have some conscious experiences we would rather have than others. For example, most of us want to avoid pain if there’s no reward from it. Therefore, we ought to take actions that reduce pain in ourselves and others, and to help each other reach the high points of the human experience.” Although this resonates more strongly with most of us than the previous example, it is still a non-sequitur; the premises are not sufficient to prove the conclusion.

You may wonder if maybe we just haven’t found the answer, that someone will come along with a solution and bridge the gap. In fact, many, including myself, have tried. But it is impossible, because it commits a category error. Is-statements are descriptive, whereas ought-statements are normative. Given a number of descriptive statements, you can derive more descriptive statements. Given a number of normative statements, you can derive more normative statements. However, it is impossible, using statements from just one category, to make conclusions that lie within the other. If you ever hear anyone claim to have solved the “is-ought problem,” all they have done is show they don’t understand it.

If we look at what is, we see all kinds of moral systems arising, competing, dying out, thriving above, or beneath, or to the side of others. From rule of the strongest to compassion for all to following the words of the hero or prophet or god or priesthood. It’s clear that moral systems exist, and people follow them passionately, and clearly have a way of determining what they should and should not do within their moral framework. It is also clear that what is true, or what they believe is true, plays a factor in it.

This shows us a sort-of exception to the is-ought gap; if we take some ought-statements as a given, then we have a goal. Once we have a goal, is-statements can show us how we ought to act in order to move toward that goal. This is true for goals that are finished once they are accomplished, as well as for the goals of acting in certain ways over periods of time. In this way, we can use is-statements together with ought-statements to derive more ought-statements. For instance, if we don’t want to be inside a burning building, then we ought to light a fire in the fireplace only if it is safe; and if the fire alarm goes off or the room starts to fill with smoke, we ought to leave the building. If we want to avoid the pain and consequences of a car crash, then if the training programs are good, we ought to receive driver training; if the rules of the road are safe, we ought to adhere to them; if insurance is worth more than the risk of a crash, we ought to have insurance; and all kinds of stuff like that. Given goals, facts about the world can help us know what we ought to do to move toward those goals.

We haven’t bridged the is-ought gap—there is still the implication that we want to be safe and avoid unnecessary suffering—but we have figured out how to use is-statements together with ought-statements to help us reach toward the things we value. There may be no way to prove with absolute certainty what we ought to do, and even if we could, it’s not reasonable to expect everyone to be experts on moral philosophy, but we can get by well enough if we inject a little common sense into the discussion and choose to work toward what we believe to be right. We’ll go more into that in the next entry of the Meta-Ethics series.

Significance – Large and Small Numbers

Toolbelt of Knowledge: Concepts
Algorithms
Equivalence
Emergence
Math
The Anthropic Principle
Substrate-Independence
Significance

Here’s a question: what do you get when you add one to a million? The answer: still a million.

Well, precisely speaking, it’s a million and one. But in the real world, it’s hardly ever necessary to be that precise. Let me put the question another way: what do you get when you add a drop of water to a full sink? The answer: still a full sink. Even if the amount of water in the sink to begin with is exactly a million times the amount in the drop, it does not change the fact that the full sink at the end is indistinguishable from the full sink at the beginning, and we call it and treat it as the same thing.

When adding a drop of water to a sinkfull, the drop is insignificant. But a single drop on a microscope slide  makes all the difference in the world. By itself, the drop is neither significant nor insignificant; we need context in order to say one way or the other.

This is a neat concept for science, but it leads to a troubling everyday question: when do your and my individual actions matter? Is there any real reason for me to personally recycle my plastics, or vote, or be a conscientious consumer? There will only be a significant impact if lots of people do it. One more or one less won’t make a difference.

This is the part where I should say, “Of course an individual’s contribution makes a difference.” And if enough people believe it, large numbers of people will do good things and a real difference will be made. There are times when a lie like this is the simplest, most harmless way to make good things happen, and I’m all for this message being spread. But here on A Scientist’s Fiction, we boldly face the truth head-on, not letting ourselves be distracted by wishful thinking. The question isn’t, “Why is it true that an individual’s contribution makes a difference?” The question is, “How do we argue that individuals should do the right thing, given the fact that an individual’s contribution does not make a difference?”

First, we should note that there are many times when individual actions do make a difference. Like a drop of water under a microscope, taking time out of your day to spend on another person, even a mere smile as you pass them by, can make a world of a difference for that person. That alone makes it worth it.

But even on the collective scale where individual actions don’t make a difference, there is still a reason to do the right thing. That reason is because you and I want to be good people. We want to be the kind of people who are responsible with our environment, with our economy, with our government. Even if taking your own bag to the grocery store is not going to make a dent in the world’s plastic problem, it is the kind of thing a good person does. It’s not just about plastic anymore, it’s about building habits of responsibility that help you in every aspect of your life. And if you can’t recycle, or if you aren’t sure which politician is the right one, the pressure is off. One person not being perfect isn’t the end of the world. So let’s do what we believe is right, regardless of whether that particular choice makes a difference in the grand scheme of things.

An Atheist's Best Argument For the Existence of God

When searching for truth, we often find that smart people are divided on the answers to any particular question. Truth, it turns out, is not always obvious, and finding it requires careful consideration of all reasonable possibilities. That’s why I’ve decided to start writing discussions about the best arguments against my points of view. We will start today with the existence of God.

I’ve written before about God the fictional archetype and God the principle of existence. The God I don’t believe in is God the real person, so that is what we will be talking about today.

There are many arguments in favor of God’s existence, some ancient, some modern. Very few, however, are persuasive to anyone who does not already believe God exists, and they are almost no one’s personal reason for their belief; rather, they are almost always used as rationalizations under the guise of “apologetics.” You can read some of them here if you would like.

Before we get to the argument I find most persuasive, let’s look at one often pointed to by other atheists, the argument from apparent design, also known as the Teleological Argument. I do not find it persuasive at all, and I will explain why. The best version of it goes like this:

A. Within the laws of physics, there are a number of parameters that sit on a razor’s edge. Just a small nudge upward or downward, and life could not exist.

Note: There are probably many configurations that would allow life of some kind, but they are vastly outnumbered by those that would not.

B. The probability that these parameters randomly landed on values that permit life is so low as to be nonexistent. It couldn’t have been coincidence.

C. Therefore, our universe was intentionally designed for life to exist.

The premises A and B are true. The universe is finely tuned for life to exist, and it couldn’t have been coincidence. But the conclusion that God made the universe does not follow from the premises. Just because it is a possible explanation doesn’t mean it is the true explanation. We also have to consider other possible explanations, and the more we find, the less likely God is to be the answer.

First, the laws of physics and the shape of our universe as we currently understand them suggest that there are at least four possible types of multiverses, each of which might have variations in the physical parameters. Perhaps even five or six, depending on how quantum gravity behaves in black holes and in higher dimensions. If even a single one of these exists, we have another possible explanation. If the chances of life existing in a given universe are 10 to the power of a big number, but the number of universes that exist are 10 to the power of a much bigger number, then there is no surprise that we exist. So if we allow the four most plausible types of multiverses as possible answers, then what the Teleological Argument really says is that there is a 1/5 chance of the universe being intentionally designed.

I want to pause for a moment and deconstruct a myth often heard from religious apologists: “Scientists posit multiverses as an excuse not to believe in God.” This is baseless slander. Multiverses are predicted results of physics theories—some of them quite well-established—or philosophical deliberations that are not related to the question of God. Physicists who want there to be only one universe have to add extra fluff to the theories in order to force the multiverses to go away; a practice that is scientifically sketchy. Furthermore, there are many scientists and other people who believe in the existence of both God and a multiverse.

Back to the argument, Multverses are not the only possible answers. If we’re going to consider intentional design as a possibility, we have to consider other supernatural explanations as well. For instance, the universe might have been unconsciously created by a sleeping God. Or, it might be impossible for conscious observers not to exist, so the universe was required by necessity to have parameters such that conscious observers would come to exist.

These possibilities mean that the real results of the Teleological Argument at best give intentional design a 1/7 chance of being the answer. That’s less than 15%. And it doesn’t factor in all of the billions of different kinds of gods and supernatural creatures which could have intentionally created the universe. It also runs into the problem of deduction: even if we could definitively rule out all of the possibilities we have thought of except for God, we could never rule out the possibility that there are more we have not thought of yet. This is why I do not find the Teleological Argument the least bit persuasive.

If the argument most people point to as the most persuasive is not persuasive at all, then what is? Well, there is one thing that keeps me questioning every once in a while. It is the same reason most believers really believe: a feeling that God is talking to me. Sometimes, I have intuitions that I should or should not do something. I don’t know why, I just know it is true. When I ignore it, I suffer. When I listen to it, things go well. These intuitions have a natural explanation: our senses take in much more information than we can consciously process, so our unconscious takes over and feeds our conscious minds its results in the form of feelings. There is also no reason to believe they are from any particular god over any other. Yet the feeling, when trained upon itself, feels like it is the voice of God. Others may not find this convincing, and it may not be rational, but to me, this is the most compelling argument for the existence of God.

Substrate-Independence – Abstract Truths Beyond Matter and Space-Time

Toolbelt of Knowledge: Concepts
Algorithms
Equivalence
Emergence
Math
The Anthropic Principle
Substrate-Independence
Significance

Substrate-independence is a term from the philosophy of consciousness, particularly information-based physicalism. It describes the hypothesis that consciousness does not depend on neurons and biology, but will exist anywhere the correct patterns of information exist. According to substrate-independence, the material doesn’t matter. If a computer, or an electrical circuit, or a network of switches, or any other substrate, could do the same thing our brains do, that system would be conscious. If the patterns in your brain were moved into one of these systems, which continued the evolution of the pattern, you would leave your body and go into that system. If this is true, then consciousness is independent of the substrate it rides upon.

I want to take the idea of substrate-independence and make it more general. If we assume consciousness is identified with something to do with information, and works on any substrate that can perpetuate that information, then why not say all information is substrate-independent? If some piece of information is stored as electrical signals on a hard drive, or in a text in a book, or a line of red and white stones, it’s the same information. The substrate doesn’t matter; it’s substrate-independent.

We can take this further, to something even more abstract: scientific models. These models are ideas: organizations or systems that are developed to describe real phenomena. You probably have an intuition for what these are, but here are some examples for clarity: the germ theory of disease, Newtonian gravity, the protoplanetary disk theory of solar system formation, information theory, the canonical ensemble of statistics, and so on.

I should note that it might not be correct to call theories substrate-independent. However, if there is a better term for what I want to describe, I don’t know it. If I come across it, this post will get an update or a revisit. For now, we’ll just go with it.

Note: I have since learned that the general term is "universality." When I get around to it, I will edit or rewrite this post with that term.

For a scientific theory to be substrate-independent, it must be generalizable. This means not all scientific theories are substrate-independent. For instance, there is nothing special about the periodic table of the elements. In another universe, it could be different. A large number of parameters could be changed, such as the charge of an electron or the range of the strong nuclear force, each of which would completely change the periodic table. The periodic table depends on a lot of things being as they are. This is true for all classifications, as far as I can tell, since they all depend on what they are describing.

But theories that describe abstract and generalizable systems are substrate-independent. Information is substrate-independent; it works on anything, in any universe. Evolution by variation and natural selection is substrate-independent. Any system that reproduces itself with changes and subject to selection pressures will follow Darwinian evolution. Life on Earth, instances in a computer program, cultural fads and values, all of these things evolve by variation and natural selection. Darwinian evolution is substrate-independent.

What about math? Addition and subtraction describe any amount of any type of thing where more are added or some are taken away. Circles describe everything whose edge is roughly the same distance from its center at all points. However, I don’t think it makes sense to say math is substrate-independent. Math is meant to describe ideas, which are not material things. Although math can be applied to physical things, it is not particularly designed to do so, and asking whether it is substrate-independent seems like asking whether a rock is too blue for you to lift it. It might make sense if we construe the definitions in just the right ways, but it’s easier to say it doesn’t apply. However, math and substrate-independent theories both apply in every possible universe, meaning they are both families of physically-transcendent truths. So I suppose whether we call math substrate-independent or not depends on personal preference.

If something is substrate-independent, it means it works no matter what material it describes or runs on, nor what universe it exists within. In fact, some substrate independent models may apply to universes themselves. Perhaps consciousness can run on computers, and perhaps it can run in other universes with alternative physics that would render everything inside them unfamiliar to us. It is calming and satisfying to know that some things are true no matter where or when, or even outside of space and time.